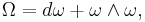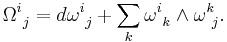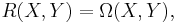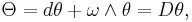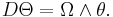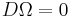Curvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.
Contents |
Definition
Let G be a Lie group with Lie algebra 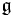 , and P → B be a principal G-bundle. Let ω be an Ehresmann connection on P (which is a
, and P → B be a principal G-bundle. Let ω be an Ehresmann connection on P (which is a 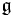 -valued one-form on P).
-valued one-form on P).
Then the curvature form is the 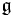 -valued 2-form on P defined by
-valued 2-form on P defined by
Here  stands for exterior derivative,
stands for exterior derivative, ![[\cdot,\cdot]](/2012-wikipedia_en_all_nopic_01_2012/I/3587c5df5edf1176ed7afc1f20f5d8a9.png) is defined by
is defined by ![[\alpha \otimes X, \beta \otimes Y]�:= \alpha \wedge \beta \otimes [X, Y]_\mathfrak{g}](/2012-wikipedia_en_all_nopic_01_2012/I/5f2ba8563c32433475d92aaff9992afd.png) and D denotes the exterior covariant derivative. In other terms,
and D denotes the exterior covariant derivative. In other terms,
Curvature form in a vector bundle
If E → B is a vector bundle. then one can also think of ω as a matrix of 1-forms and the above formula becomes the structure equation:
where 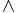 is the wedge product. More precisely, if
is the wedge product. More precisely, if 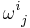 and
and 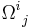 denote components of ω and Ω correspondingly, (so each
denote components of ω and Ω correspondingly, (so each 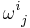 is a usual 1-form and each
is a usual 1-form and each 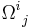 is a usual 2-form) then
is a usual 2-form) then
For example, for the tangent bundle of a Riemannian manifold, the structure group is O(n) and Ω is a 2-form with values in o(n), the antisymmetric matrices. In this case the form Ω is an alternative description of the curvature tensor, i.e.
using the standard notation for the Riemannian curvature tensor,
Bianchi identities
If  is the canonical vector-valued 1-form on the frame bundle, the torsion
is the canonical vector-valued 1-form on the frame bundle, the torsion 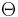 of the connection form
of the connection form  is the vector-valued 2-form defined by the structure equation
is the vector-valued 2-form defined by the structure equation
where as above D denotes the exterior covariant derivative.
The first Bianchi identity takes the form
The second Bianchi identity takes the form
and is valid more generally for any connection in a principal bundle.
References
- S.Kobayashi and K.Nomizu, "Foundations of Differential Geometry", Chapters 2 and 3, Vol.I, Wiley-Interscience.
See also
- Connection (principal bundle)
- Basic introduction to the mathematics of curved spacetime
- Chern-Simons form
- Curvature of Riemannian manifolds
- Gauge theory
|
||||||||||||||
![\Omega=d\omega %2B{1\over 2}[\omega,\omega]=D\omega.](/2012-wikipedia_en_all_nopic_01_2012/I/d4a93453ea87eb7c3ff88befabc1a1eb.png)
![\,\Omega(X,Y)=d\omega(X,Y) %2B [\omega(X),\omega(Y)].](/2012-wikipedia_en_all_nopic_01_2012/I/fe6c7e22df693b08fee79e3043c64c0f.png)